二分法好写,但bug颇多。
记住二分法的思想:每次舍弃答案一定不存在的区间,保留答案存在的区间。同时注意二分区间状态转移的一致性。
题单:https://leetcode.cn/studyplan/binary-search/
有序不重复数组
默认中点取法向下取整,则 $left \le mid <right$,这点的影响在这尚未体现。
简单二分
单调递增数组找目标元素下标,元素不重复,目标元素不在其中则返回-1。
https://leetcode.cn/problems/binary-search/description/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public int search(int[] nums, int target) {
int l=0, r=nums.length -1;
while(l <= r){
int mid = (l+r)/2;
if(nums[mid] == target) return mid;
if(nums[mid] < target)
l = mid + 1;
else
r = mid - 1;
}
return -1;
}
}
|
看起来很简单,修改下题目,得到以下这题
搜索插入位置
单调递增数组找目标元素下标,元素不重复,如果元素不在其中,返回元素应该在插入的下标。
比如数组【1】,元素0返回下标0,元素1返回下标0,元素2返回下标1。
https://leetcode.cn/problems/search-insert-position/
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public int searchInsert(int[] nums, int target) {
int l=0, r=nums.length-1;
while(l<=r){
int mid=l+(r-l)/2;
if(nums[mid]<target)
l=mid+1;
else
r=mid-1;
}
return l;
}
}
|
这题如果沿用上题的左闭右闭区间表示法,就会发现困难重重,其根本原因就在左闭右闭区间无法包括所有答案应在的位置,比如,[1,2,3] 搜索 4 所在位置。仔细揣摩以上代码,虽然写得很精巧,但其中的逻辑转变不是很直观。
我更推荐以下写法:
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public int searchInsert(int[] nums, int target) {
int l = 0, r = nums.length;
while(l < r){
int mid = (l+r)/2;
if(nums[mid]>=target)
r = mid;
else
l = mid+1;
}
return l;
}
}
|
将每一次缩小区间的过程看成一次状态转移:从一个大区间到一个小区间,其中状态转移的一致性就是指永远保留答案在我的窗口区间内(每次舍弃答案不在的区间)。
那么我们就能对比 while(l <= r) 和 while(l < r)的区别了。由于第一题采用左闭右闭区间表示法,在l==r时仍然能构成小区间,那么答案是可能在这个区间内的,我们还需要继续在这个区间搜索下去。
第二题的while(l < r)同理,在nums[mid]>=target 时,应该往左边缩小区间,r应该为mid-1吗?不应该,因为这样答案可能不在这个区间。举例子[1,3]或[1,2]数组中搜索2所在位置。
这样第一题和第二题就构成了逻辑上的统一。
有序重复数组
排序数组寻找元素第一个和最后一个位置
https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| class Solution {
public int lower_bound(int[] nums, int target){
int l = 0, r = nums.length;
while(l<r){
int mid = (l+r)/2;
if(nums[mid]>=target)
r = mid;
else
l = mid +1;
}
return l;
}
public int upper_bound(int[] nums, int target){
int l = 0, r = nums.length;
while(l<r){
int mid = (l+r)/2;
if(nums[mid]>target)
r = mid;
else
l = mid +1;
}
return l;
}
public int[] searchRange(int[] nums, int target) {
int[] ans = {-1, -1};
int l = lower_bound(nums, target);
if(l==nums.length || nums[l]!=target) return ans;
int r = upper_bound(nums, target);
ans[0] = l;
ans[1] = r-1;
return ans;
}
}
|
Lower_bound 的语义:有序重复数组寻找目标元素第一次出现的位置,如果不存在,返回应该插入的位置。
Upper_bound 的语义:有序重复数组寻找大于目标元素的数字第一次出现的位置,如果不存在,返回应该插入的位置。
换位思考:先求序列中第一个大于x的元素的位置,然后减1就是x最后出现的位置。
upper bound对于targer极大,只能返回N,所以需要合理使用。或者使用以下思路:
1
2
3
4
5
6
7
8
9
| public int[] searchRange(int[] nums, int target) {
int[] ans = {-1, -1};
int l = lower_bound(nums, target);
if(l==nums.length || nums[l]!=target) return ans;
int r = lower_bound(nums, 1+target);
ans[0] = l;
ans[1] = r-1;
return ans;
}
|
泛化
通过思考可以发现,lower和upper函数都在解决这样一个问题:在一个有序序列中第一个满足某条件的元素的位置。
lower-bound就是,从左到右,找第一个满足“值大于等于target”的元素。
upper-bound就是,从左到右,找第一个满足“值大于target”的元素。
于是就有了这样一个模版:
1
2
3
4
5
6
7
8
9
10
11
|
int solve(int left, int right){
while(left < right){
int mid = (left+right)/2;
if(条件成立)
right = mid;
else
left = mid+1;
}
return left;
}
|
这个函数解决在某序列中,从左到右,第一个满足条件的元素下标。
比如求最后一个x<4的元素下标,数组为[1,2,2,2,5],答案为3
先求第一个满足x>=4的下标,为4,然后减去1,得到答案3
题目
keke吃香蕉
https://leetcode.cn/problems/koko-eating-bananas/description/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
public int solve(int[] piles, int speed){
int time = 0;
for(int banana: piles){
time += (banana+speed-1)/speed;
}
return time;
}
public int minEatingSpeed(int[] piles, int h) {
int l =1, r = -1;
for(int pile:piles){
r = Math.max(r, pile);
}
while(l < r){
int mid = (l+r)/2;
int time = solve(piles, mid);
if(time<=h){
r = mid;
}else{
l = mid+1;
}
}
return r;
}
}
|
最小速度可以为1,但1不保证能在h小时吃完所有香蕉。最大速度怎么求?无限大?只要找到一个能在h小时吃完所有香蕉的速度speed就行。这个speed是个上界,但不是上确界。
小技巧:上取整的实现
1
| int time = p/s + (p%s>0) ? 1:0;
|
货物运输
https://leetcode.cn/problems/capacity-to-ship-packages-within-d-days/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| class Solution {
public int transit(int[] weights, int load){
int day = 0;
int cur = 0;
for(int weight:weights){
if(cur+weight <load){
cur += weight;
}else if(cur+weight ==load){
++day;
cur = 0;
}
else{
++day;
cur = weight;
}
}
if(cur>0) ++day;
return day;
}
public int shipWithinDays(int[] weights, int days) {
int l =0, r=0;
for(int weight:weights){
r += weight;
l = Math.max(l , weight);
}
System.out.println(transit(weights, 5));
while( l < r){
int mid = l + (r-l)/2;
int day = transit(weights, mid);
if(day <= days){
r = mid;
}else{
l = mid+1;
}
}
return r;
}
}
|
这题与上面一题几乎一样!注意点:
1、左右边界的确定
左边界是weights的最大,因为船至少能装一个货物。最大就是求和,这样能在一天运完。
2、计算当前负载需要天数的函数
用模拟方式进行,负载装满就出发。
旋转排序数组中的最小值
https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array/description/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution {
public int findMin(int[] nums) {
int l=0, r=nums.length-1;
if(nums[l]<=nums[r]) return nums[l];
while(l<r && nums[l]>nums[r]){
int mid = (l+r)>>1;
if(nums[mid]>=nums[l]){
l = mid+1;
}else{
r = mid;
}
}
return nums[l];
}
}
|
在应用二分法时,每次缩小区间,其实是排除不符合条件的区间过程。
旋转排序数组,其实是分成了两个有序段,左半段和右半段,左半段的值肯定是大于右半段的值。但这题的难点在于左右两段的情况可能不存在,以及应用二分法的过程中,可能从两个段跨越到一个段,导致语义错误。
那么我就应用状态机的思想,维持我left和right的区间始终为两个段的情况(nums[l]>nums[r]),如果跨越到右半段,直接返回右半段的最左边的值。
这道题的难点还在于mid究竟是要和left还是right进行比较?
(1)mid和right比较没问题。如果nums[mid]>nums[right],那么mid肯定落在左半段。如果nums[mid]<=nums[right],那么mid是落在右半段。
(2)mid和left比较有风险!left可能越过最高点,整个区间从两个段变成一个段,再也不能通过nums[mid]>=nums[left]来判断mid是落在左半段还是右半段(因为落到单升序区间后,nums[mid]>nums[left]的条件指示我们往右走的行为已经违背了题目初衷)。所以 while(l<r && nums[l]>nums[r]) 这里条件中nums[l]>nums[r] 必不可少的,这是要保持l,r窗口内是失序的状态,一旦打破,就达到了有序状态,直接返回最左边界的值。
(3)那为什么mid和right比较没问题?因为即使left可能越过最高点,整个区间变成有序状态后,不会再出现nums[mid]>nums[right]的情况。
贴上mid和right比较的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public int findMin(int[] nums) {
int l=0, r=nums.length-1;
while(l<r){
int mid = (l+r)>>1;
if(nums[mid] < nums[r]){
r = mid;
}else{
l = mid+1;
}
}
return nums[l];
}
}
|
最后需要注意的一点,mid和left比较的代码是大于等于,和right比较是小于(小于等于也行)。
因为在mid的计算过程中, $left \le mid <right$,是会出现left!=right,但是mid==left的情况。此时left和mid可能构成一个单独的段,要确保这个段能被捕捉到。
搜索旋转排序数组
给你一个target,在旋转排序数组中找它的下标,不存在返回-1。
https://leetcode.cn/problems/search-in-rotated-sorted-array/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public int search(int[] nums, int target) {
if(nums==null||nums.length==0) return -1;
int l=0, r=nums.length-1;
while(l<=r){
int mid = (l+r)>>1;
if(nums[mid] == target) return mid;
if(nums[l] <= nums[mid]){
if(nums[l] <= target && target < nums[mid]){
r = mid-1;
}else{
l = mid+1;
}
}else{
if(nums[mid] < target && target <= nums[r]){
l = mid+1;
}else{
r = mid-1;
}
}
}
return -1;
}
}
|
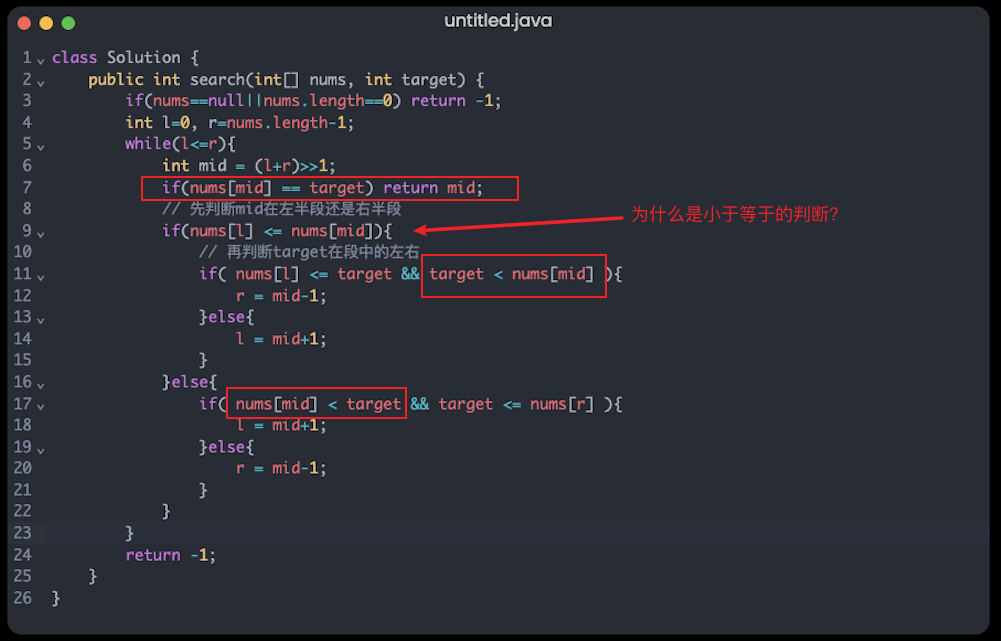
nums数组旋转前就是个升序不重复的数组,然后只需要判断元素是否在这个数组中,用左闭右闭的区间表示正合适。
nums[l] <= nums[mid] 用小于等于比较是为了构成有效区间。也可以和right进行比较,见下方代码,两者语义是一致的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public int search(int[] nums, int target) {
if(nums==null||nums.length==0) return -1;
int l=0, r=nums.length-1;
while(l<=r){
int mid = (l+r)>>1;
if(nums[mid] == target) return mid;
if(nums[mid] <= nums[r]){
if(nums[mid] < target && target <= nums[r]){
l = mid+1;
}else{
r = mid-1;
}
}else{
if(nums[l] <= target && target < nums[mid]){
r = mid-1;
}else{
l = mid+1;
}
}
}
return -1;
}
}
|
搜索旋转排序数组2
给你一个target,在旋转排序数组(这个数组可能含有重复元素)中找它的下标,不存在返回-1。
https://leetcode.cn/problems/search-in-rotated-sorted-array-ii/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
public boolean search(int[] nums, int target) {
if(nums==null||nums.length==0) return false;
int l=0, r=nums.length-1;
while(l<=r){
int mid = (l+r)>>1;
if(nums[mid] == target) return true;
if(nums[l] == nums[mid]) {l++;continue;}
if(nums[l] < nums[mid]){
if(nums[l]<= target && target < nums[mid]){
r = mid-1;
}else{
l = mid+1;
}
}else{
if(nums[mid]<target && target<=nums[r]){
l = mid+1;
}else{
r = mid-1;
}
}
}
return false;
}
}
|
这里比上题就多出了一行代码
1
| if(nums[l] == nums[mid]) {l++;continue;}
|
总结
在应用二分法,注意左右边界的获取。
根据区间的表示法,选择合适while循环判断条件。
在应用二分法时,每次缩小区间,其实是排除不符合条件的区间过程。
状态转移的一致性就是指永远保留答案在我的窗口区间内(每次舍弃答案不在的区间)。

