实验P2

实验二要求实现一个数据结构 ：B+树。

实验难点在于理清B+树存储结构、插入分裂、删除合并以及并发控制。

强烈建议阅读教材给出的B+树执行流程的伪代码。

B+树细节

B+树的阶数

m阶B+树，即内部结点最多m个子树。参考教材可以得到：

• 根结点最少2个孩子，最多m个孩子。根结点既可以是内部结点，也可以是叶子结点。

• 内部结点最少有$\lceil m/2\rceil$ 孩子，最多m个孩子。

• 叶子结点的键值对最少有$\lceil (m-1) /2\rceil$ ，最多m-1。

当根节点是叶子结点时（即当前B+树只有一个结点），根节点最多存储m-1个键值对；当根节点为内部结点时，根节点可以存储最多m个键值对。

从定义上我们可以窥见：B+树的结点总是不太满又不太少（大于一半），这就有很好的页利用率。

tips: 上取整数的实现技巧 ⌈x/2⌉ = ⌊(1+x)/2⌋

阶数与实现关系

（1）数组存储

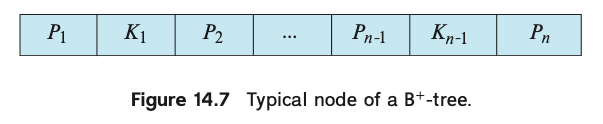
在键值对的存储上，内部结点和叶子结点都采用一个键值对数组的方式。

#define MappingType std::pair<KeyType, ValueType>
MappingType array_[1];
// 可以理解为
vector<pair<key, value>> array; 

• 内部结点的key就是泛化的键（用于索引比较），value则是指向下一个页的指针（本次实验则是存储下一个页的页ID）。
• 叶子结点的key是泛化的键，value就是一个RecordID，RecordID包括PageID和SlotNum（表示一条记录在一个页内的偏移）。
• Pm所在的子树上所有键都小于Km，大于等于Km-1

采取RecordID是间接存储行记录的方式，也有直接存储，即将整个行记录存在value中的方式。

在实现上为了维护内部结点指针比键多一的特性，内部结点的数组的第一个元素的key设置为空。

回到实验代码上，结点会有size和max_size属性表示当前数组的长度和最大长度。

size_	4	Number of Key & Value pairs in page
max_size_	4	Max number of Key & Value pairs in page

#define LEAF_PAGE_HEADER_SIZE 28
#define LEAF_PAGE_SIZE ((BUSTUB_PAGE_SIZE - LEAF_PAGE_HEADER_SIZE) / sizeof(MappingType))

#define INTERNAL_PAGE_HEADER_SIZE 24
#define INTERNAL_PAGE_SIZE ((BUSTUB_PAGE_SIZE - INTERNAL_PAGE_HEADER_SIZE) / (sizeof(MappingType)))

从宏定义上也能看出，默认的数组的最大长度由一个页减去头部字段大小然后除以kv对计算得到。

（2）阶数与数组最大长度关系

INDEX_TEMPLATE_ARGUMENTS
BPLUSTREE_TYPE::BPlusTree(std::string name, BufferPoolManager *buffer_pool_manager, const KeyComparator &comparator,
                          int leaf_max_size, int internal_max_size)
    : index_name_(std::move(name)),
      root_page_id_(INVALID_PAGE_ID),
      buffer_pool_manager_(buffer_pool_manager),
      comparator_(comparator),
      leaf_max_size_(leaf_max_size),
      internal_max_size_(internal_max_size) {}

在B+树的构造函数中，会传入叶子结点的最大长度和内部结点的最大长度。

BPlusTree<GenericKey<8>, RID, GenericComparator<8>> tree("foo_pk", bpm, comparator, 2, 3);

并且在测试代码中，可以看到这两个最大长度并不是一致的。

问题：为什么这两个size为不一样？

答：因为叶子结点和内部结点存的东西不一样，一张页的大小是固定的，自然计算出的size不一样。

问题2：阶数到底是哪一个？是leaf_max_size_还是internal_max_size_？

答：这里我觉得无需介意，在固定页大小背景下， 这两个都是能真实存储的极限大小，实现上满足内部结点和叶子结点的语义即可。

• 内部结点的语义是：给定大小m，我的数组长度最小为$\lceil m/2\rceil$ ，最多m，即我可以占满整个页空间。
• 叶子结点的语义是：给定大小m，我的数组长度最小$\lceil (m-1) /2\rceil$ ，最多m-1，即我的数组最长时，在整个页空间上留下一个空位。

问题3：为什么要留下一个空位，而不是存满？

答：想象一下，在数据库的存储中，假设一个页最多存M个数据，叶子页可以存满M个。我现在有一个满叶子页L，此时插入的新数据K正好索引到L上，页满需要页分裂。页分裂的过程：创建新页，然后将M+1个数据平分到两个页上。但是，你需要先将K插入到M个数据上的合适位置，这就要求申请存储M+1个数据大小的内存空间。而一个页最多存M个数据，这就很别扭。而留下空位的做法，使得最后一个位置的元素可以充当哨兵，可以做到先插入再分裂。插入数据结束后，检查叶子页大小是否已满，已满则进行分裂。

问题4：为什么内部页可以存满？

答： 因为内部页的第一个元素的key是未使用的（牵强）

插入过程伪代码

插入过程需要注意的是：

• 叶子结点分裂时，中间键作为索引是复制一份插入到parent。而内部结点分裂时，中间键直接被拿走，插入parent中。

• 内部页分裂时必须及时更新孩子结点的父亲指向

删除过程伪代码

删除过程比较复杂，内部结点的删除和中间结点的删除需要单独处理。大致逻辑是从叶子结点删除完一个元素后，如果元素太少，那么就需要和周围结点合并为一个结点，或者重新分配元素（无法合并为一个结点的情况）。最后别忘记更改父亲的指针，整个过程从下往上进行。

重分配的过程是从邻居结点借一个元素的过程。

B+树节点页的交互

B+树的节点页是以嵌套的方式存储在页的data区域，通过buffer pool manager进行交互。

auto* p = reinterpret_cast<LeafPage*>(buffer_pool_manager_->FetchPage(page_id)->GetData());

B+树并发

基本思想

主要思想为像螃蟹一样横着走路，意为先跨出去一步踩稳后，再收回一步。体现在B+树中就是从当前结点N开始获得锁，然后在获得N的儿子C的锁。如果C是安全的，那么就可以释放N的锁。（A thread can only release latch on a parent page if its child page considered “safe”. ）

根据操作的不同，结点安全也有不同的解释：

• 对于插入操作，只有当前size小于GetMaxSize() - 1才是安全的
• 对于删除操作，只有当前size大于GetMinSize()才是安全的

基本的螃蟹锁协议：

• 查找：从根结点开始，获得儿子结点的共享锁后释放父结点的共享锁。
• 插入/删除：从根结点开始，获得儿子结点的排它锁 。然后检查儿子的安全性，如果儿子节点是安全的，则释放儿子结点的所有祖先结点的锁。否则一直持有锁。

注意这里儿子结点安全后是释放所有祖先结点的锁。如果只释放父结点的锁的话，会出现锁得不到释放的现象。比如ABCD的遍历顺序，A是安全根结点，BC是不安全结点，D是安全结点，根据规则，我们将一直持有锁遍历到D，如果只释放父结点的锁，那么AB的锁就得不到释放。

优化思想

The problem with the basic latch crabbing algorithm is that transac- tions always acquire an exclusive latch on the root for every insert/delete operation

基本的螃蟹锁思想缺点是插入与删除操作都要先获得根结点的排它锁，这导致并行度不高。

一种优化的思想是采用乐观锁的思想，插入与删除操作都先采用共享锁一路爬到叶子结点，然后校验叶子结点的安全性。如果叶子是安全的，采用排它锁完成更新。如果叶子节点不安全，则放弃所有共享锁，从根结点开始一路获取排它锁。

• Search: Same algorithm as before.
• Insert/Delete: Set READ latches as if for search, go to leaf, and set WRITE latch on leaf. If the leaf is not safe, release all previous latches, and restart the transaction using previous Insert/Delete protocol.

书本18.10描述的螃蟹锁规则/协议：

When searching for a key value, the crabbing protocol first locks the root node in shared mode. When traversing down the tree, it acquires a shared lock on the child node to be traversed further. After acquiring the lock on the child node, it releases the lock on the parent node. It repeats this process until it reaches a leaf node.

When inserting or deleting a key value, the crabbing protocol takes these actions:

° It follows the same protocol as for searching until it reaches the desired leaf node. Up to this point, it obtains (and releases) only shared locks.

° It locks the leaf node in exclusive mode and inserts or deletes the key value.

° If it needs to split a node or coalesce it with its siblings, or redistribute key values between siblings, the crabbing protocol locks the parent of the node in exclusive mode. After performing these actions, it releases the locks on the node and siblings.

If the parent requires splitting, coalescing, or redistribution of key values, the protocol retains the lock on the parent, and splitting, coalescing, or redistri- bution propagates further in the same manner. Otherwise, it releases the lock on the parent.

• 搜索键值时，crabbing 协议首先将根节点锁定为共享模式。向下遍历树时，它会在子节点上获取共享锁，以便进一步遍历。获取子节点上的锁后，它会释放父节点上的锁。它会重复此过程，直到到达叶节点。

• 插入或删除键值时，Crabbing 协议会执行以下操作：

  • 它遵循与搜索相同的协议，直到到达所需的叶节点。到目前为止，它只获取（和释放）共享锁。

  • 将叶节点锁定为独占模式，并插入或删除键值。

  • 如果它需要拆分节点或将其与其同级合并或在同级之间重新分配密钥值，则 crabbing 协议会以独占模式锁定节点的父节点。执行这些操作后，它会释放节点和同级上的锁。

    如果父级需要拆分、合并或重新分发密钥值，则协议将保留对父级的锁定，并且拆分、合并或重新分配会以相同的方式进一步传播。否则，它将释放父项上的锁。

leaf node scan问题

前述加锁方式都是top-down自顶向下式的，一个线程只能获得当前结点的儿子结点的锁，如果不能获得，就必须等待。

但如果一个线程从一个叶子移动到另外一个叶子，就会出现死锁的情况。此时，需要靠程序进行死锁预防/避免。no-wait原则要求一个线程获得锁失败时释放它所有拥有的锁，然后重新开始尝试。

前置知识点

flexible array

柔性数组，可自适应空间大小，避免固定空间浪费。

具体特点：

• 柔性数组为结构体的最后一个成员；
• 该结构体至少包含一个非柔性数组成员；
• 编译器支持C99标准。

 typedef struct {
     int32_t id;
     int32_t grade;
     int8_t name[];
 }student_info_struct;
// 使用方式
int8_t *name = "sdc";
si = (student_info_struct *)malloc(sizeof(student_info_struct) + strlen(name) + 1); 

数组名作为地址，可以自适应占据分配给结构体的空间，实现动态扩张。

好处：直接分配结构体和缓冲区大小，避免两次分配（一次结构体，一次缓冲区）

踩坑/经验

Root page id的更新

void BPLUSTREE_TYPE::UpdateRootPageId(int insert_record);

当第一次创建根结点时，我们需要向header page插入一条root page id的记录，即使用UpdateRootPageId(1);

此后，更新根结点但树不变，采用UpdateRootPageId(0);

InternalPage 和 leafPage 的更新

（1）数组

这两个page的array的是不一样的，内部页第一个key为空，leaf则存满。

在实现插入/删除/构造新page的API时，这两个不一样的array常常使得我的下标计算错误，出现各种莫名bug。

（2）叶子是链表关系，内部页是树关系

在分裂过程中，叶子结点要额外维护链表指针关系；内部页则要维护树关系（及时更新child的parent pointer指向）。

页管理

page的缓存管理是个大难题，因为我们要手动进行抓取和释放页面的管理（FetchPage和 UnpinPage）。

在实践中，我总结出了两种页管理的机制：

• 谁fetch，谁unpin；
• 谁最后一次用page，谁unpin。

首先我们需要知道释放一个页面的时机是什么。答案是：这个页面不用时。

（1）谁fetch，谁unpin

这个的思想在于让第一次fetch的函数作为页面负责人，由它进行释放页面。好比于小明向图书馆借了一本书，然后小明又将这本书借给同学A、同学B、同学C，最后小明还要负责从C手上拿回书，然后小明将书还给图书馆。

INDEX_TEMPLATE_ARGUMENTS
auto BPLUSTREE_TYPE::Insert(const KeyType &key, const ValueType &value, Transaction *transaction) -> bool {
	....
  auto leaf_page = FindLeafPage(key, Operation::INSERT, transaction);
  auto *leaf_node = reinterpret_cast<LeafPage *>(leaf_page);

	...
  InsertInParent(risen_key, leaf_node, sibling_leaf_node, transaction);
	...
    
  buffer_pool_manager_->UnpinPage(leaf_node->GetPageId(), true);
  buffer_pool_manager_->UnpinPage(sibling_leaf_node->GetPageId(), true);
  return true;
}

在代码中，实际上是函数嵌套的情况，最后一次拿回书的过程其实不用实现。

（2）谁最后一次用page，谁unpin

这个思想应该很好懂了， 结合上面的代码，那么InsertInParent应该负责leaf_node和sibling_leaf_node的页面释放。

（3）意外情况 / 辅助函数设计

在实际实现中，我们会有一个findLeaf的函数，它需要找到叶子页面并交出去。显然这个findLeaf的函数并不能很好地适合第一种页管理的原则，因为它抓取了页面，却不能管理页面的释放。

但是我们这样想就简单多了：将findLeaf视作一个大fetch的函数，其他函数使用它就相当于抓取页面，最后由其他函数负责释放。

迭代器

迭代器就是简单的单向链表遍历，只有查找的API，比较容易实现。实现过程犯的错：

• 在创建迭代器时忘记判断树是否为空，未及时返回END迭代器

• 辅助函数没有设置树空的判断，导致出现逻辑错误。

并发控制

（1）锁存储

由于需要“释放之前持有的锁”这一操作，我们需要一个顺序容器来存储锁，这点请看transaction里的page_set_成员。

（2）锁管理与页管理

锁管理依然有两种方式：

• 谁加锁，谁负责释放锁
• 谁最后一次用锁，谁负责释放锁

但是实现螃蟹锁的过程中，我们管理的其实是page的队列，这要求我们一并管理页面：在队列里拿到page，释放这个page的锁，然后释放这个page。

（3）root page id锁

为了代码锁里的简洁，可以添加一个root page id锁，作为root结点的“前置锁”。相当于一个伪根结点，这样判断结点安全的逻辑就很顺畅了：默认我们持有前一个页面锁和现在的结点，再判断结点是否安全后，再释放前一个页面锁或将之添加到锁队列中。

开发经验

实验中涉及多个代码文件，虽然实验指导上写着先实现B+树的page，但实际上此时根本不知道怎么设计API。而且这时臆想的接口与直接写B+树时大相径庭。实现中辅助函数是多变的。

src/include/storage/page/b_plus_tree_page.h
src/storage/page/b_plus_tree_page.cpp
src/include/storage/page/b_plus_tree_internal_page.h
src/storage/page/b_plus_tree_internal_page.cpp
src/include/storage/page/b_plus_tree_leaf_page.h
src/storage/page/b_plus_tree_leaf_page.cpp
src/include/storage/index/b_plus_tree.h
src/storage/index/b_plus_tree.cpp
src/include/storage/index/index_iterator.h
src/storage/index/index_iterator.cpp

开发思路：自顶向下，先填充主干，再丰满细节。

• b_plus_tree_page.h
• b_plus_tree_internal_page.h
• b_plus_tree_leaf_page.h

以上头文件写函数签名，暂时不要考虑实现。

然后在b+树的实现文件b_plus_tree.cpp里将整个函数流程实现，遇到辅助函数就在相应头文件定义。最后再去补充各个头文件的实现，最后再补齐b_plus_tree.h的函数签名。