发表更新数据结构与算法 / 动态规划26 分钟读完 (大约3951个字)

动态规划

笔记来自代码随想录，题目加自己题解。

动态规划五部曲

  • 确定dp数组下标含义

  • 确定递推公式（状态转移）

  • dp数组初始化

  • 确定遍历顺序

  • 举例推导

一周目 基础题目

二周目 背包问题

只讲两个关键问题：01背包和完全背包。

两种dp数组：二维dp和一维dp（滚动数组、空间优化）

两种遍历方式：物品遍历和背包遍历；前向遍历和后向遍历。

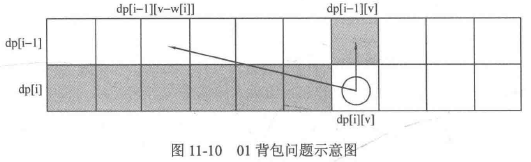
01背包问题

从最简单的01背包问题讲起。有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

dp[i][v]表示从前i（0～i）件物品中任意选取，装入容量为v的背包，能获得的最大价值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//第0件物品初始化
for (int j = 0 ; j < weight[0]; j++)  //小于weight0的装不下
    dp[0][j] = 0; 
for (int j = weight[0]; j <= bagweight; j++) 
    dp[0][j] = value[0];


// 递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
// 前i件物品，选不选第i件
// 先遍历物品再遍历背包
for(int i = 1; i < weight.size(); i++) { // 遍历物品，weight数组的大小 就是物品个数
    for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
        if (j < weight[i]) 
          dp[i][j] = dp[i - 1][j];
        else 
          dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
    }
}

二维数组的空间优化：滚动数组

可以从递推公式中看到，第i个物品的状态只与第i-1个物品的状态相关。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//可以看成两层，上一层是历史状态，计算完dp[i][v]后dp[i-1][v]就再也用不到了，可以被覆盖
//从右往左才不会影响到历史状态
for (int i = 1; i <= n; i++) {
    for (int v = V; v >= w[i]; v--) { //必须逆序
        dp[v] = max(dp[v],dp[v-w[i]] + c[i]);
    }
}

//代码随想录
void test_1_wei_bag_problem() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagWeight = 4;

    // 初始化
    vector<int> dp(bagWeight + 1, 0);
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    cout << dp[bagWeight] << endl;
}

思考：能不能先遍历背包容量，再遍历物品呢？即改变两个for循环的位置

答案是不行，改变位置后，每个dp【j】只会放入价值最高的物品，只有一个物品。（j被i重复迭代，只会放入价值最高物品）

相关题目

分割等和子集

https://leetcode.cn/problems/partition-equal-subset-sum/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public boolean canPartition(int[] nums) {
        int sum = 0;
        for(int num: nums)
            sum+=num;
        if(sum%2==1) return false;
        int bagWeight = sum/2;
        int[][] dp = new int[nums.length][bagWeight+1];
        // 初始化
        for(int j=0; j<=bagWeight; ++j){
            if(j>=nums[0]) dp[0][j] = nums[0];
            else dp[0][j] = 0;
        }
        for(int i=1; i<nums.length; ++i){
            for(int j=0; j<=bagWeight; ++j){
                if(j<nums[i])
                    dp[i][j] = dp[i-1][j];
                else
                    dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-nums[i]]+nums[i]);
            }
        }
        // System.out.println(Arrays.deepToString(dp));
        return dp[nums.length-1][bagWeight]==bagWeight? true:false;
    }
}
  • 背包容量为集合总和的一半，每个元素可以选取一次，就相当于01背包
  • 第一次做有点抽象，细想，求背包能装的最大容量，肯定会遍历所有元素

最后一块石头的重量

https://leetcode.cn/problems/last-stone-weight-ii/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
lass Solution {
    public int lastStoneWeightII(int[] stones) {
        // 分成尽可能相近的两堆
        int sum = 0;
        for(int stone: stones) sum+=stone;
        int bagWeight = sum/2;
        int[][] dp = new int[stones.length][bagWeight+1];
        for(int j=0; j<=bagWeight; ++j)
            if(j>=stones[0]) dp[0][j] = stones[0];
        for(int i=1; i<stones.length; ++i){
            for(int j=0; j<=bagWeight; ++j){
                if(j < stones[i])
                    dp[i][j] = dp[i-1][j];
                else
                    dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-stones[i]]+stones[i]);
            }
        }
        return sum-2*dp[stones.length-1][bagWeight];
    }
}
  • 这题体现了循序渐进的作用了，如果没做分割等和子集这道题，可能想不到
  • 实际上就是分为重量接近的两堆石头，两个石头相撞后大的石头还是留在原来那一堆

目标和

https://leetcode.cn/problems/target-sum/‘

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        //dp[i][j] 表示i件东西装满j的背包有多少种装法
        int sum = 0;
        for(int num: nums) sum+=num;
        if((sum+target)%2==1) return 0;
        if(sum < Math.abs(target)) return 0;
        int bagWeight = (sum+target)/2;
        int[][] dp = new int[1+nums.length][bagWeight+1];
        dp[0][0] = 1; //容量0的背包装0件物品，一种装法
        for(int i=1; i<= nums.length; ++i){
            for(int j=0; j<=bagWeight; ++j){
                if(j>=nums[i-1]) 
                    dp[i][j] = dp[i-1][j]+dp[i-1][j-nums[i-1]];
                else
                    dp[i][j] = dp[i-1][j];
            }
        }
        System.out.println(Arrays.deepToString(dp));
        return dp[nums.length][bagWeight];
    }
}
  • 还是循序渐进的作用。初看题目？可能没什么思绪。其实还是分成两部分，一部分为+号，另一部分为-号，通过数学运算就能得出背包的容量
  • 这道题不同的地方在于求数目。装满背包有多少种方法。
  • dp【j】 = dp【j】+dp【j-num【i】】 ，不选物品的方法数+选物品的方法数

一和零

https://leetcode.cn/problems/ones-and-zeroes/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int zeros(String s){
        int count = 0;
        for(int i=0; i<s.length(); ++i)
            if(s.charAt(i) == '0') count++;
        return count;
    }
    public int ones(String s){
        int count = 0;
        for(int i=0; i<s.length(); ++i)
            if(s.charAt(i) == '1') count++;
        return count;
    }
    public int findMaxForm(String[] strs, int m, int n) {
        // 三维背包-> 二维做法
        int[][] dp = new int[1+m][1+n];
        int oneNum = ones(strs[0]);
        int zeroNum = zeros(strs[0]);
        // for(int i = zeroNum; i<=m; ++i)
        //     for(int j= oneNum; j<=n; ++j)
        //         dp[i][j] = 1;
        for(int k=0; k<strs.length; ++k){
            int onex = ones(strs[k]);
            int zerox = zeros(strs[k]);
            for(int i=m; i>=zerox; --i)
                for(int j=n; j>=onex; --j)
                    dp[i][j] = Math.max(dp[i][j], 1+dp[i-zerox][j-onex]);    
        }
        System.out.println(Arrays.deepToString(dp));
        return dp[m][n];
    }
}
  • 这道题相当于两个维度的背包，0的个数是一个维度，1的个数是一个维度
  • 又因为一个字符串是一起放入的，所以状态转移的时候少了很多状态
  • dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);

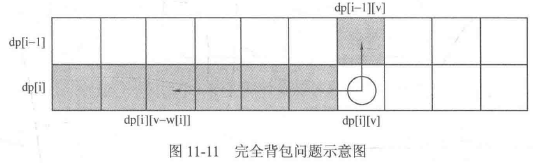
完全背包问题

在完全背包问题中，每种物品有无限个，可以无限选取。写成二维形式的话，取了i件物品还能再取。求将哪些物品装入背包里物品价值总和最大。

dp[i][v] = max(dp[i-1][v], dp[i][i-w[i]]+c[i])

简化为 一维形式的话，公式和01背包一摸一样，不同的是正向枚举。

1
2
3
4
5
for (int i = 1; i <= n; i++) {
    for (int v = w[i]; v <=V; v++) {
        dp[v] = max(dp[v], dp[v - w[i]] + c[i];
    }
}

理解正向枚举：

在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序是无所谓的！

1
2
3
4
5
6
7
8
// 先遍历背包，再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        if (j - weight[i] >= 0) 
          dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
    cout << endl;
}

相关题目

组合总和

https://leetcode.cn/problems/combination-sum-iv/

1
2
3
4
5
6
for(int i=1; i<target; ++i){
	for(int num:nums){
		if(i-num>=0)
 			dp[i] = dp[i] + dp[i-num];
 	}
}

初始时，dp[i]为0，dp[i-num]可以看成最后一步跳num步台阶到达第i阶楼梯的方法数，这样就保证了分成的子问题互相不重叠。

零钱兑换

https://leetcode.cn/problems/coin-change-ii/description/

  • 标准的完全背包，但不同的是求装满背包的组合数
  • 该怎么办呢？先遍历物品再遍历背包！
  • 先遍历物品保证了背包装入物品的顺序性，怎么理解？

比如遍历到第i个物品的时候，我们看转移方程

1
2
3
4
5
for (int i = 0; i < coins.size(); i++) { // 遍历物品
    for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量
        dp[j] = dp[j] + dp[j - coins[i]];
    }
}

转移方程的后半部分保证了在背包容量为j时，dp[j] + dp[j - coins[i]] 是由0。。。i-1等物品组成背包方法数。

完全平方数

https://leetcode.cn/problems/perfect-squares/

  • 给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, …）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

  • 完全背包问题，但是要求最少数量，因此要初始化为INT MAX

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int numSquares(int n) {
        // n 是背包容量， sqrt（n）是物品个数
        int[] dp = new int[1+n];
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = 0;
        for(int i=1; i<=n; ++i){
            for(int j=1; j*j<=i; ++j){
                dp[i] = Math.min(dp[i], 1+dp[i-j*j]);
            }
        }
        return dp[n];
    }
}

单词拆分

https://leetcode.cn/problems/word-break/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        boolean[] dp = new boolean[s.length()+1];
        dp[0] = true;
        for(int i=1; i<=s.length(); ++i){
            for(String word : wordDict){
                if(word.length() <= i){
                    String postfix = s.substring(i-word.length(), i);
                    if(postfix.equals(word)){
                        dp[i] =  dp[i] || dp[i-word.length()];
                    }
                }
            }
        }
        return dp[s.length()];
    }
}
  • 拆分时可以重复使用字典中的单词，说明就是一个完全背包！
  • 先遍历物品，再遍历背包
  • 回溯法记忆搜索，待做//todo

三周目 打家劫舍+股票问题

打家劫舍系列问题

打家劫舍1

https://leetcode.cn/problems/house-robber/

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int rob(int[] nums) {
        int[] dp = new int[nums.length];
        if(nums.length<=1) return nums[0];
        dp[0] = nums[0];
        dp[1] = Math.max(nums[0], nums[1]);
        for(int i=2; i<nums.length; ++i){
            dp[i] = Math.max(dp[i-1], dp[i-2]+nums[i]);
        }
        return dp[nums.length-1];
    }
}
  • 只能隔着一家偷，因此 dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);

打家劫舍2

https://leetcode.cn/problems/house-robber-ii/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int robRange(int[] nums, int l, int r){
        int[] dp = new int[nums.length];
        dp[l] = nums[l];
        dp[l+1] = Math.max(nums[l], nums[l+1]);
        for(int i=l+2; i<r; ++i){
            dp[i] = Math.max(dp[i-1], dp[i-2]+nums[i]);
        }
        return dp[r-1];
    }
    public int rob(int[] nums) {
        if(nums.length==1) return nums[0];
        if(nums.length==2) return Math.max(nums[0], nums[1]);
        int a1 = robRange(nums, 1, nums.length); // 不偷起始家
        int a2 = robRange(nums, 0, nums.length-1); // 不偷最后一家
        return Math.max(a1, a2);
    }
}

环形队列，考虑偷的起始点。假设编号为0、1、2..N，那么偷第0家后，第N家必定不能偷，问题可以转为为0到N-1的打家劫舍问题。

同样地，由于第0家可偷可不偷，不偷第0家，问题就是1到N的打家劫舍问题。

打家劫舍3

https://leetcode.cn/problems/house-robber-iii/

（1）记忆化搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public Map<TreeNode, Integer> map = new HashMap<>();
    public int rob(TreeNode root) {
       if(root==null) return 0;
       if(map.containsKey(root)) return map.get(root);
       // 取root节点的值
       int ans1 = root.val;
       if(root.left!=null) ans1+= rob(root.left.left)+rob(root.left.right);
       if(root.right!=null) ans1+= rob(root.right.left)+rob(root.right.right);
       // 不取root节点的值
       int ans2  = rob(root.left) + rob(root.right);
       int ans = Math.max(ans1, ans2);
       map.put(root, ans);
       return ans; 
    }
}

基于数组的DP往往是线性的，而树形状的DP还是利用函数递归+记忆化搜索更合适。

（2）优化-树形DP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int[] dpTree(TreeNode root){
        int[] ans = new int[2]; // 两种状态，偷与不偷
        if(root==null) return new int[]{0,0};
        int[] left = dpTree(root.left);
        int[] right = dpTree(root.right);
        // 不偷root
        ans[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
        // 偷root
        ans[1] = left[0]+right[0]+root.val;
        return ans;
    }
    public int rob(TreeNode root) {
        int[] ans = dpTree(root);
        return Math.max(ans[0], ans[1]); 
    }
}

这种写法将偷与不偷这两种状态合在一个数组中，然后在自底向上的更新。这是树形DP的技巧，见动态规划进阶。

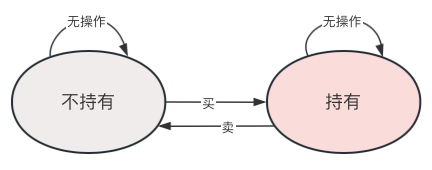
买卖股票问题

买卖股票问题引入了状态转移，需要画图辅佐思路。

买卖股票的最佳时机1

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int maxProfit(int[] prices) {
        int[][] dp = new int[prices.length][3];
        dp[0][0] = 0; //不持有股票的最大现金
        dp[0][1] = -prices[0]; //首次持有股票的最大现金
        dp[0][2] = 0; //首次卖出的最大现金
        for(int i=1; i<prices.length; ++i){
            dp[i][0] = dp[i-1][0];
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0]-prices[i]);
            dp[i][2] = Math.max(dp[i-1][2], dp[i-1][1]+prices[i]);
        }
        // System.out.println(Arrays.deepToString(dp));
        return dp[prices.length-1][2];
    }
}

本题限制只能买卖股票一次，因此卖出股票后就不能再继续操作。

每一天引入三种状态：不持有股票、持有股票、首次卖出股票。每种状态具有几种操作，每种操作又能把第k天的状态变为第k+1天的状态。

买卖股票的最佳时机2

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/

（1）动态规划解法

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int maxProfit(int[] prices) {
        int[][] dp = new int[prices.length][2];
        dp[0][0] = -prices[0]; //第k天必定持有股票时最大现金，股票可以在前k天买入一次
        dp[0][1] = 0; //第k天不持有股票的最大现金
        for(int i=1; i<prices.length; ++i){
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1]-prices[i]); //不做操作、买入操作
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0]+prices[i]);  // 不做操作、卖出操作
        }
        // System.out.println(Arrays.deepToString(dp));
        return dp[prices.length-1][1];
    }
}

只有两种状态：不持有股票、持有股票。

（2）贪心解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int maxProfit(int[] nums) {
        // 当天买，如果第二天价格高就卖，否则换成第二天买
        int hold = nums[0];
        int ans = 0;
        for(int i=1; i<nums.length; ++i){
            if(nums[i]>hold){
                ans += nums[i]-hold; 
                hold = nums[i];
            }else if(nums[i]< hold){
                hold = nums[i];
            }
        }
        return ans;
    }
}

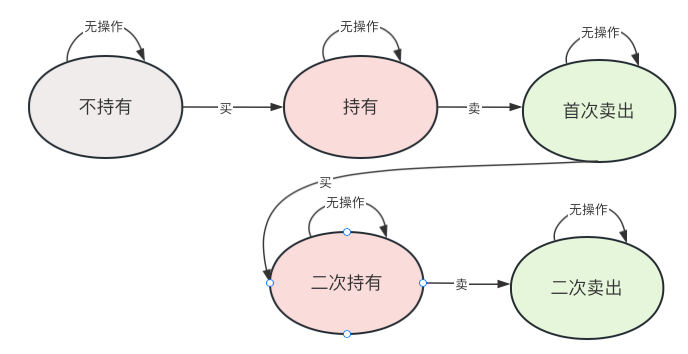
买卖股票的最佳时机3

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        vector<vector<int>> dp(prices.size(), vector<int>(5, 0));
        dp[0][1] = -prices[0]; // 一次操作持有股票
        dp[0][2] = 0;  //一次操作卖出股票 
        dp[0][3] = dp[0][2] - prices[0]; //二次操作持有股票，注意这里
        dp[0][4] = 0;  // 二次操作卖出股票
        for(int i=1; i<prices.size(); ++i){
            dp[i][0] = dp[i-1][0];
            dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i]);
            dp[i][2] = max(dp[i-1][2], dp[i-1][1] + prices[i]);
            dp[i][3] = max(dp[i-1][3], dp[i-1][2] - prices[i]);
            dp[i][4] = max(dp[i-1][4], dp[i-1][3] + prices[i]);
        }
        return dp[prices.size()-1][4];
    }
};

这道题限制最多买卖两次。

  • 五种状态：不持有股票，首次持有股票、首次卖出股票、第二次持有股票、第二次卖出股票；

  • 注意二次持有股票时的初始化与一次持有一样，这是为了收集答案时，获得最大收益时，出售股票不一定恰好是两次。

买卖股票的最佳时机4

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv/

  • 引入2k+1种状态

买卖股票的最佳时机5

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-cooldown/

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int maxProfit(int[] prices) {
        int N = prices.length;
        int[][] dp = new int[N][4];
        dp[0][1] = -prices[0];
        for(int i=1; i<prices.length; ++i){
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][3]);
            dp[i][1] = Math.max(dp[i-1][1], Math.max(dp[i-1][0]-prices[i], dp[i-1][3]-prices[i]));
            dp[i][2] = dp[i-1][1]+prices[i];
            dp[i][3] = dp[i-1][2]; 
        }
        return Math.max(dp[N-1][2], Math.max(dp[N-1][3], dp[N-1][0]));
    }
  • 有四种状态：不持有股票、持有股票、冷冻期、自由期

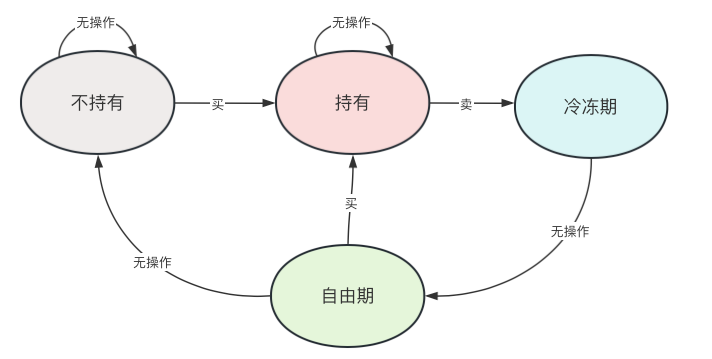
每种状态都是自身描述，由当前天的操作转移到第二天的状态。因此持有股票当前天卖出，第二天为冷冻期。冷冻期无操作第二天是自由期。

买卖股票含手续费

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/

  • 没啥好说的，同买股票2

画出状态转移图，一切不在话下！

四周目 字符串dp

子串、子序列、编辑距离、回文串

子串和子序列问题

kanade算法 求最大子串和

最长公共子串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class Solution {
    public String LCS (String str1, String str2) {
        int[][] dp = new int[1+str1.length()][1+str2.length()];
        int len = 0;
        int start = -1;
        //dp[0][0] = 1;
        for(int i=1; i<=str1.length(); ++i){
            for(int j=1; j<=str2.length(); ++j){
                if(str1.charAt(i-1)==str2.charAt(j-1)){
                    dp[i][j] = 1 + dp[i-1][j-1];
                }
                if(dp[i][j] > len){
                    len = dp[i][j];
                    start = i - len;
                }
            }
        }
        return str1.substring(start, start+len);
    }
}

dpij不能简单的设置为以i，j结尾两个字符串的最长公共子串长度，因为不知道这个公共子串的开始位置和结束位置。所以要设置为公共子串恰好以ij结尾。不匹配的话dpij就是0。

编辑距离系列

判断子序列

https://leetcode.cn/problems/is-subsequence/

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public boolean isSubsequence(String s, String t) {
        int[][] dp = new int[1+s.length()][1+t.length()];
        for(int i=1; i<=s.length(); ++i){
            for(int j=1; j<=t.length(); ++j){
                if(s.charAt(i-1) == t.charAt(j-1))
                    dp[i][j] = 1 + dp[i-1][j-1];
                else
                    dp[i][j] = dp[i][j-1];
            }
        }
        return dp[s.length()][t.length()]==s.length();
    }
}

本题最好的解法是双指针，子序列只要求顺序一致，两个指针分别遍历一边s和t，时间复杂度在O（n+m）。

但为了编辑距离的抛砖引玉，确定dp数组的含义：dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度

以及递推公式的含义：

  • if (s[i - 1] == t[j - 1])
    • t中找到了一个字符在s中也出现了（这相当于从后向前匹配）
  • if (s[i - 1] != t[j - 1])
    • 相当于t要删除元素，继续匹配

最难理解的就是s[i - 1] == t[j - 1])的情况，其实是从后向前匹配！

  • 时间复杂度：O(n × m)
  • 空间复杂度：O(n × m)

不同的子序列

https://leetcode.cn/problems/distinct-subsequences/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int numDistinct(String s, String t) {
        int[][] dp = new int[1+s.length()][1+t.length()];
        for(int i=0; i<=s.length(); ++i)
            dp[i][0] = 1;
        // for(int j=0; j<=t.length(); ++j)
        //     dp[0][j]=0;
        for(int i=1; i<=s.length(); ++i){
            for(int j=1; j<=t.length(); ++j){
                if(s.charAt(i-1) == t.charAt(j-1))
                    dp[i][j] = dp[i-1][j] + dp[i-1][j-1];
                else
                    dp[i][j] = dp[i-1][j];
            }
        }
        return dp[s.length()][t.length()];
    }
}

dp数组的含义仍然：dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度

不过不同的是si与tj匹配成功后，tj其实有两种匹配方法：匹配最后一个，或者最后一个不匹配，向sj-1匹配。

对应 dp[i][j] = dp[i-1][j] + dp[i-1][j-1];，小例子：s=babgba，t=b

特别要注意的是初始化的过程：dp【i】【0】全都为1，因为0自然匹配成功。

两个字符串的删除

https://leetcode.cn/problems/delete-operation-for-two-strings/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int minDistance(String s, String t) {
        int[][] dp = new int[1+s.length()][1+t.length()];
        for(int i=0; i<=s.length(); ++i)
            dp[i][0] = i;
        for(int j=0; j<=t.length(); ++j)
            dp[0][j] = j;
        for(int i=1; i<=s.length(); ++i){
            for(int j=1; j<=t.length(); ++j){
                if(s.charAt(i-1) == t.charAt(j-1))
                    dp[i][j] = dp[i-1][j-1];
                else
                    dp[i][j] = 1 + Math.min(dp[i-1][j], dp[i][j-1]);
            }
        }
        return dp[s.length()][t.length()];
    }
}

dp数组仍然是题目中的含义。让我们想一想失配的含义，自然是删除s中的一个，然后去与t匹配，或者删除t中的一个去与s匹配。对应 dp[i][j] = 1 + Math.min(dp[i-1][j], dp[i][j-1]);

匹配成功时，由于能够删除任意一个字符串的中一个字符，直接忽略这个字符就好了。

编辑距离

https://leetcode.cn/problems/edit-distance/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int minDistance(String s, String t) {
        int[][] dp = new int[1+s.length()][1+t.length()];
        for(int i=0; i<=s.length(); ++i)
            dp[i][0] = i;
        for(int j=0; j<=t.length(); ++j)
            dp[0][j] = j;
        for(int i=1; i<=s.length(); ++i){
            for(int j=1; j<=t.length(); ++j){
                if(s.charAt(i-1) == t.charAt(j-1))
                    dp[i][j] = dp[i-1][j-1];
                else{
                    dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]);
                    dp[i][j] = Math.min(dp[i][j], dp[i-1][j-1]);
                    dp[i][j] ++; // 删除、替换操作 
                }
            }
        }
        return dp[s.length()][t.length()];
    }
}

虽然三种操作看着吓人，但仔细想想，增加操作就等价于删除（为什么？）

仍然考虑失配场景：si与tj匹配不成功。

  • 替换操作：将si与tj替换为相同的字母，找下一步s[i-1]和t[i-1]

  • 删除操作：删除si或tj，对应找dp[i-1][j], dp[i][j-1])

  • 增加操作；我在si处增加一个字母，那么接下来怎么匹配？自然是si与ti-1匹配，因为ti已经匹配了。这不就是相当于删除ti吗？

明白这点后，题目也就不难了。

回文串

回文串就要利用回文串的性质，左右对称，因此可以从中间展开，也有双指针的解法。

回文子串

https://leetcode.cn/problems/palindromic-substrings/

给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int countSubstrings(String s) {
        int N = s.length();
        int ans = 0;
        boolean[][] dp = new boolean[N][N];
        // dp[i][j] means s[i] to s[j] is phadorme
        for(int i=0; i<N; ++i){
            for(int j=0; j<=i; ++j){
                if(s.charAt(i) == s.charAt(j)){
                    if(i-j<=1)
                        dp[j][i] = true;
                    else
                        dp[j][i] = dp[j+1][i-1];
                }
                if(dp[j][i]) ans++;
            }
        }
        return ans;
    }
}

最长回文子串

https://leetcode.cn/problems/longest-palindromic-substring/description/

给你一个字符串 s，找到 s 中最长的回文子串。

(1)动态规划（常规写法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public String longestPalindrome(String s) {
        int l=0,r=0;
        int N = s.length();
        boolean[][] dp = new boolean[N][N];
        //dp[j][i] 表示j, i间为回文字符串
        for(int i=0; i<N; ++i){
            for(int j=0; j<=i; ++j){
                if(s.charAt(i)==s.charAt(j)){
                    if(i-j<=1)
                        dp[j][i] = true;
                    else
                        dp[j][i] = dp[j+1][i-1];
                }
                if(dp[j][i] && i- j> r-l){ // 长度大于之前的
                    l = j;
                    r = i;
                }
            }
        }
        return s.substring(l, r+1);
    }
}

(2)动态规划（以长度遍历，更容易理解的写法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public String longestPalindrome(String s) {
        int l=0,r=0;
        int N = s.length();
        boolean[][] dp = new boolean[N][N];
        for(int len=1; len<=N; ++len){
            for(int i=0; i<N && i+len-1<N; ++i){
                int j = i+len-1; // 从i开始，长度为len的串
                if(s.charAt(i) == s.charAt(j))
                    dp[i][j] = (i==j) || (i+1==j) || dp[i+1][j-1];
                if(dp[i][j] && j-i>r-l){
                    r = j;
                    l = i;
                }
            }
        }
        return s.substring(l, r+1);
    }
}

(3)双指针（空间效率O（1）的解法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public int[] find(String s, int l, int r){
        while((l-1>=0) && (r+1<s.length()) && (s.charAt(l-1)==s.charAt(r+1))){
            --l;
            ++r;
        }
        int r_l = l;
        int r_r = r;
        return new int[]{r_l, r_r};
    }
    public String longestPalindrome(String s) {
        int l=0, r=0;
        for(int i=0; i<s.length(); ++i){
            int[] odd = find(s, i, i); //奇数长度回文串
            int[] even = {0,0};
            if(i+1< s.length() && s.charAt(i)==s.charAt(i+1))
                even = find(s, i, i+1); // 偶数长度回文串

            if(r-l < odd[1]-odd[0]){
                l = odd[0];
                r = odd[1];
            }
            if(r-l < even[1]-even[0]){
                l = even[0];
                r = even[1];
            }
        }
        return s.substring(l, r+1); 
    }
}

注意：substring函数是从l到r，最后一个索引不包含。

最长回文子序列 https://leetcode.cn/problems/longest-palindromic-subsequence/

  • 给定一个字符串 s ，找到其中最长的回文子序列，并返回该序列的长度。

分割回文串的最小次数

https://leetcode.cn/problems/palindrome-partitioning-ii/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    int minCut(string s) {
        //dp[i] means samllest segment times
        vector<int> dp(s.size(), 0);
        for(int i=0; i<s.size(); ++i) dp[i]=i;
        // precaculate the whole string
        vector<vector<int>> ispalindromic(s.size(), vector<int>(s.size(), 0));
      	//打表记录i，j是否是回文子串，也是动态规划的体现
        for (int i = s.size()-1; i>=0; --i){
            for (int j = i; j < s.size(); ++j){
                if(s[i]==s[j]){
                    if(j-i<=1) ispalindromic[i][j]=1;
                    else  ispalindromic[i][j] = ispalindromic[i+1][j-1];
                }
            }
        }
 }
        //递推进行
        for(int i=1;i<s.size();++i){
            if(ispalindromic[0][i]){
                dp[i]=0;
                continue;
            }else{
                for(int j=0;j<i;j++){
                    if(ispalindromic[j+1][i])
                        dp[i] = min(dp[i], 1+dp[j]);
                }
            }

        }
        return dp[s.size()-1];
    }
};

动态规划

https://xyz.desirer233.fun/2024/05/30/数据结构与算法/动态规划/Java动态规划/

作者

Desirer

发布于

2024-05-30

更新于

2024-05-30

许可协议

分类

×