本节内容来自《算法笔记》-胡凡,属于动态规划入门内容。
从斐波那契数列谈起
从斐波那契数列的递归图中可以看到重叠子问题被计算多次。
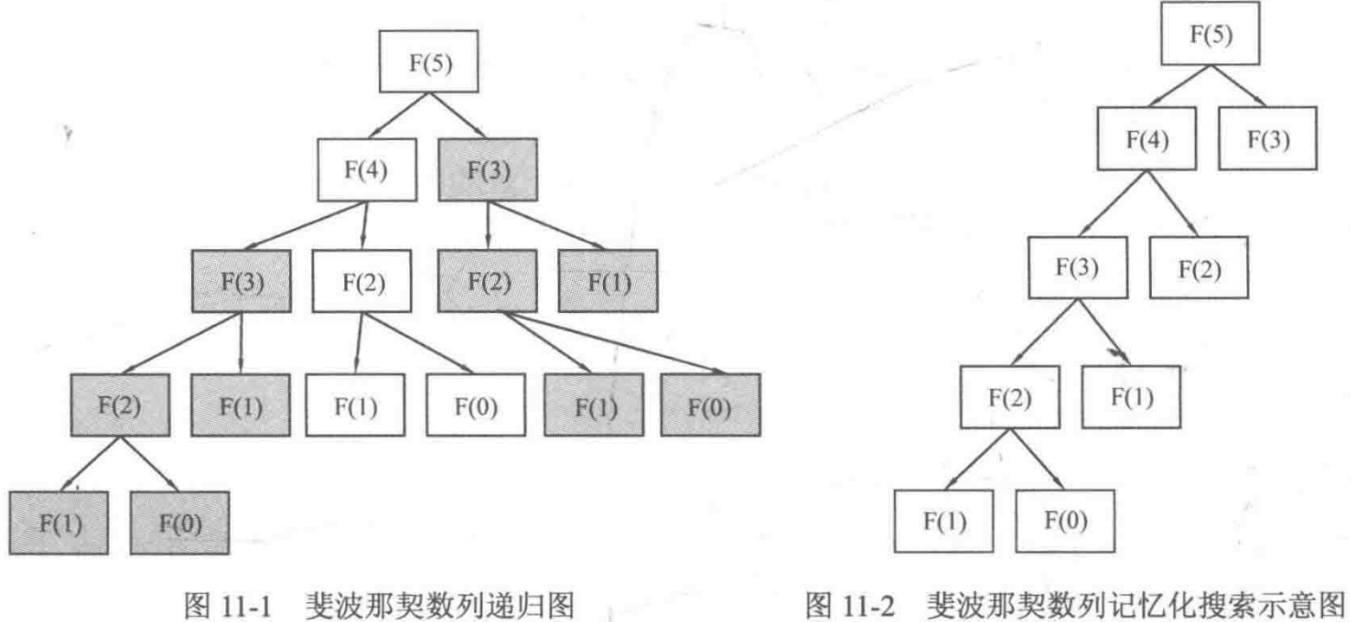
从上图中可以看到,黑色部分被计算多次。我们可以开辟一个数组,记录下第一次计算问题的解,然后再次遇到时,直接查表。这其实就是一种缓存的思想。
动态规划,最重要的是问题可重复利用(重叠子问题,如果子问题互不相交,那么不能重复利用)。
动态规划与记忆化搜索二者本质是一样的,动态规划利用新开辟的数组记录子问题的解,从而达到记忆化的效果。
从数塔问题看起
自顶向下思路
仔细思考,数塔的形状是否和斐波那契递归图很像?如果令dp[i][j]表示从第i行第j列数字到最底部的最小路径,那么就有dp[i][j] = min(dp[i+1][j], dp[i+1][j+1]) + triangle[i][j]。
第i层的状态依赖于i+1层,这样就引出来状态转移这个名词。
同时容易想到dp数组的初始化边界,最后一层当然是它自己。最后求解的问题答案就是dp[1][1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int N = triangle.size();
int[][] dp = new int[N][N];
for(int i=0; i<triangle.get(N-1).size(); ++i)
dp[N-1][i] = triangle.get(N-1).get(i);
for(int i=N-2; i>=0; --i){
for(int j=0; j<triangle.get(i).size(); ++j){
dp[i][j] = Math.min(dp[i+1][j], dp[i+1][j+1]) + triangle.get(i).get(j);
}
}
return dp[0][0];
}
}
|
自底向上思路
分治+递归。
此时dp[i][j]不能直接求解答案,而是子问题的解。
注意:这里的分治并不是严格意义上的分治,分治法要求子问题不重叠,我这里只是借助分治的意思。
最后要经历诸如 $min(dp[0], dp[1], …, dp[N])$ 的步骤,即收集子问题的解来解决原问题。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int N = triangle.size();
int[][] dp = new int[N][N];
dp[0][0] = triangle.get(0).get(0);
for(int i=1; i<N; ++i){
int i_length = triangle.get(i).size()-1;
int i_minus_length = triangle.get(i-1).size()-1;
dp[i][0] = dp[i-1][0] + triangle.get(i).get(0);
dp[i][i_length] = dp[i-1][i_minus_length] + triangle.get(i).get(i_length);
}
for(int i=1; i<N; ++i){
for(int j=1; j<triangle.get(i).size()-1; ++j){
dp[i][j] = Math.min(dp[i-1][j], dp[i-1][j-1])+triangle.get(i).get(j);
}
}
int ans = dp[N-1][0];
for(int j=1; j<triangle.get(N-1).size(); ++j){
ans = Math.min(ans, dp[N-1][j]);
}
return ans;
}
}
|
最优子结构
通过这个问题再次引出一个名词 最优子结构, 即原问题的最优解可以由子问题的最优解推导出来。
动态规划解决的问题必须是拥有重叠子问题和最优子结构。分治法解决的问题是不重叠的。
1
2
3
4
5
6
| 总结:动态规划的主要步骤
1. 设计dp数组含义
2. 找到递推公式
3. 初始化
4. 递推,并找出答案
|
例题
最大连续子序列和
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public int maxSubArray(int[] nums) {
int[] dp = new int[nums.length];
dp[0] = nums[0];
int ans = dp[0];
for(int i=1; i<nums.length; ++i){
dp[i] = Math.max(dp[i-1], 0) + nums[i];
ans = Math.max(ans, dp[i]);
}
return ans;
}
}
|
这道题属于连续子串的问题。还是上面的思路:分治+动规。
dp[i]表示以i结尾的连续子数组的最大和。
那么dp[i]就有两种思路:要么和前面一起组成连续子串,要么自己单独成立连续子串。
1
2
3
| dp[i] = max{A[i], dp[i-1] + A[i]};
dp[0] = A[0];
|
最后还要收集子问题的解。
1
| max(dp[0], dp[1], ..., dp[N])
|
最长不下降子序列
1
2
3
4
5
6
7
8
9
10
11
12
| class Solution {
public int findLengthOfLCIS(int[] nums) {
int[] dp = new int[nums.length];
dp[0] = 1;
int ans = 1;
for(int i=1; i<nums.length; ++i){
dp[i] = nums[i]>nums[i-1]?(dp[i-1]+1):1;
ans = Math.max(ans, dp[i]);
}
return ans;
}
}
|
这道题属于子序列的问题。还是上面的思路:分治+动规。
dp[i]表示以i结尾的最长不下降子序列。由于是子序列,不要求连续,那么第i个元素就可以和先前i-1个元素进行比较,整体复杂度$O(N^2)$
对比,最长连续不下降子序列 https://leetcode.cn/problems/longest-continuous-increasing-subsequence/description/
最长公共子序列
1
2
3
4
5
6
7
8
9
10
11
12
| class Solution {
public int findLengthOfLCIS(int[] nums) {
int[] dp = new int[nums.length];
dp[0] = 1;
int ans = 1;
for(int i=1; i<nums.length; ++i){
dp[i] = nums[i]>nums[i-1]?(dp[i-1]+1):1;
ans = Math.max(ans, dp[i]);
}
return ans;
}
}
|
求两个字符串的最长公共部分。两个字符串,容易想到二维dp数组。
dp[i][j]表示的是以第i个字符结尾的第一个字符串和以第j个字符结尾的第二个字符串之间的最长公共子序列的长度。

类似:最长重复子数组 https://leetcode.cn/problems/maximum-length-of-repeated-subarray/
最长回文子串
这道题有些不一样了,虽然是单个字符串,但是用一维dp数组反而不好解题。
考虑dp[i][j],表示第i个字符到第j个字符之间表示的字符串是否为回文串。
注意:这里经过两层抽象,一层是二维dp,另一层二维dp不是直接求解问题(它表示的区间字符串是否是回文串,而不是说当前区间的最长的回文串的长度),相当于前述的分治+动规
通过考虑区间长度的问题进行遍历,这其实又是一层抽象,不容易想到。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| class Solution {
public String longestPalindrome(String s) {
int l=-1,r=-1,maxLen=-1;
int N = s.length();
int[][] dp = new int[N][N];
for(int i=0; i<N; ++i){
dp[i][i] = 1;
l = i;
r = i;
}s
for(int i=0; i<N-1; ++i){
if(s.charAt(i) == s.charAt(i+1)){
dp[i][i+1] = 1;
l = i;
r = i+1;
}
}
for(int len=2; len<N; ++len){
for(int i=0; i<N-len; ++i){
if(s.charAt(i) == s.charAt(i+len)){
dp[i][i+len] = dp[i+1][i+len-1]==1? 1:0;
}
else{
dp[i][i+len] = 0;
}
if(dp[i][i+len]==1){
if(len+1 > maxLen){
maxLen = len+1;
l = i;
r = i+len;
}
}
}
}
return s.substring(l, r+1);
}
}
|
对比,最长回文子序列 https://leetcode.cn/problems/longest-palindromic-subsequence/
背包问题
背包和完全背包,重中之重。见动态规划进阶。
总结
字符串dp的套路
字符串问题涉及两个概念:子串和子序列
一般来说,子串是连续的,子序列是不连续的。如此,一种题可以出两道。
最大子串和
最大子序列和(其实就是选正数)
最长不下降子串
最长不下将子序列
最长公共子串
最长公共子序列
最长回文子串
最长回文子序列
字符串dp设计的套路
当题目与子序列或子串相关时,可以考虑一下dp的设计
(1)一维dp
- 令dp[i]表示以s[i]结尾或开头的xxxx
- dp[i]表示字符串前i个的性质
前者限定问题求解必须包含第i个元素,后面不作限定,只需要利用前i个元素求解即可。
(2)二维dp涉及两个字符串
- 令
dp[i][j]表示以s[i]结尾,以t[j]结尾的xxx
(3)二维dp只涉及一个字符串,比如求回文串
- 令
dp[i][j]表示s[i]至s[j]区间的xxx

