贪心算法,以一个局部最优来靠近全局最优。
一周目 开胃小菜
分发饼干
https://leetcode.cn/problems/assign-cookies/
很简单的思路,饼干和胃口排序。升序,类似合并链表。小饼干满足小胃口。
摆动序列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
public int wiggleMaxLength(int[] nums) {
int period = 0;
int ans = 0;
int guard = nums[0];
for(int i=1; i<nums.length;++i){
if(nums[i]>guard){
if(period==-1 || period==0) {
ans++;
period = 1;
}
}
else if(nums[i]<guard){
if(period==1 || period==0){
ans++;
period = -1;
}
}
guard = nums[i];
}
return ans+1;
}
}
|
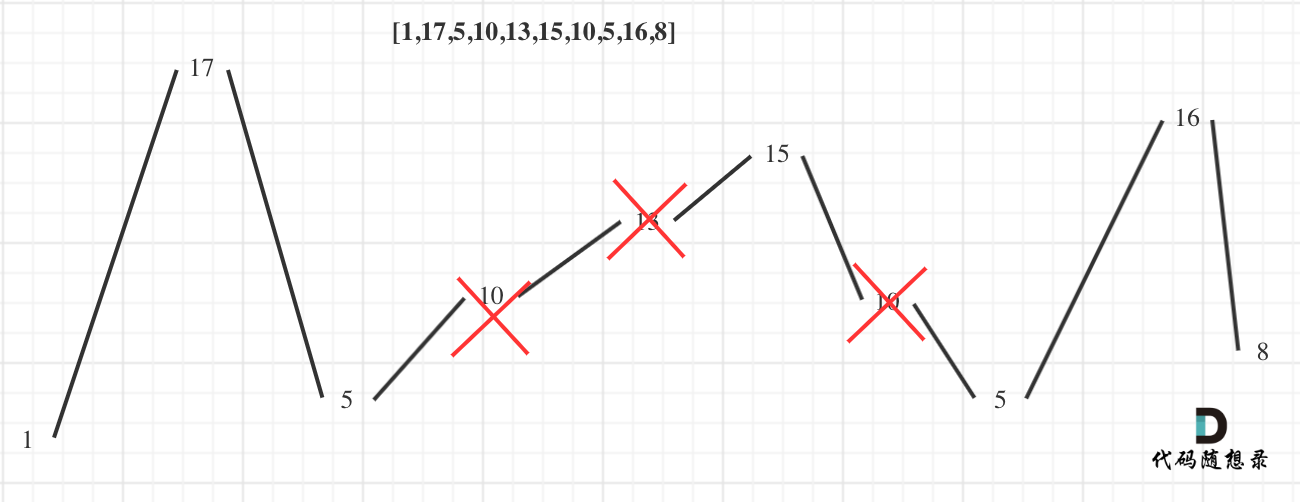
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。给定一个整数序列,返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
贪心法:考虑坡度,上坡取头尾两个数,平坡合并为一个数,下坡也只取头尾。
最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
1
2
3
| - 输入: [-2,1,-3,4,-1,2,1,-5,4]
- 输出: 6
- 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6
|
贪心法:从左到右,类似滑动窗口。窗口内和大于0仍旧右移。如果窗口内和小于0,窗口从下一个数字开始(left移到i+1)。
思考贪心法的正确性:假设最大和的连续子数组左下标为left,右下标为right。那么 任何在0,left-1这段区间内,以left-1为右边界的连续子数组的和都不会大于0。(否则最大和的连续子数组可以拓展),那么这个滑动窗口必然覆盖到解!
二周目 贪心的递归(状态转移)
买卖股票的最佳时机
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Solution {
public int maxProfit(int[] nums) {
int hold = nums[0];
int ans = 0;
for(int i=1; i<nums.length; ++i){
if(nums[i]>hold){
ans += nums[i]-hold;
hold = nums[i];
}else if(nums[i]< hold){
hold = nums[i];
}
}
return ans;
}
}
|
贪心思路:可以把第x天买,第y天卖,拆成每天一卖。
我们希望获得每个“上坡”的收益,如果第二天价格更高,那就卖。如果第二天价格低,那就放弃第一天的买入。
跳跃游戏
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public boolean canJump(int[] nums) {
if (nums.length == 1) return true;
int coverRange = 0;
for (int i = 0; i <= coverRange; i++) {
coverRange = Math.max(coverRange, i + nums[i]);
if (coverRange >= nums.length - 1) return true;
}
return false;
}
}
|
贪心思路: 每次取能跳跃的最右边界。在这左右边界内,取能跳到的最右边,作为下一个右边界。下一个左边界为当前右边界+1.
跳跃游戏2
给定一个非负整数数组,你最初位于数组的第一个位置。数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public int jump(int[] nums) {
if(nums.length<=1) return 0;
int step = 1;
int begin =0, end =nums[0];
int farest = 0;
while(end<nums.length-1){
for(int i=begin; i<=end; ++i){
farest = Math.max(farest, i+nums[i]);
}
begin = end;
end = farest;
step++;
}
return step;
}
}
|
辨析:这次要求用最少的跳跃次数。和上题思路一致,当前区间找下一个区间的最大覆盖。只不过上题是一步一步走,这次要精确的跳到最大覆盖。
三周目 贪心策略
加油站
将油量减去消耗量,得到一个数组。如果这个数组和为0,肯定不能环绕一圈。问题是,如果数组和大于等于0,一定能环绕一圈吗?
证明:数组和大于0,必定存在一个区间和大于0的区间(否则所有区间和都小于0,数组和小于0,矛盾)。这里的区间指尽可能往左右延伸,使得区间和大于零。
- 如果只存在一个区间和大于0的区间,从这个区间起点出发,必定能环绕一周。
- 如果存在多个区间和大于0的区间。(不存在)
- 我们找长度最短的区间I,且I的和大于等于0.这个区间的左右均为负数。
- 所有区间+左边元素,必定和小于0,矛盾
因此只要找到区间和大于0的区间就行。
分发糖果
这题比较有趣,引出了一个策略:多次贪心。
第一次贪心:从左到右。使得每个孩子与它左边的孩子满足题目要求。
第二次贪心:从右到左。使得每个孩子与它右边的孩子满足题目要求。
这样两边的要求就都满足了。
根据身高重建队列
这题很有意思,知道每个人的身高,以及多少个人的身高比它高。<身高,序列号>
自然而然想到排序。按什么排序呢?升序还是降序?
如果按序列号排,序列号小的排前面,序列号大的排后面。后续怎么调整?虽然说这样满足了一些序列号的性质。
按身高排序,从高到低。那么即使后面的人插入前面的人的队列中,前面的人的序列号也不会受到影响(因为后面的人的身高低),这样就提供了一种可供调整的方式。
重排字符串
给定一个字符串 s ,检查是否能重新排布其中的字母,使得两相邻的字符不同。
https://leetcode.cn/problems/reorganize-string/description/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
public String reorganizeString(String S) {
char[] alphabetArr = S.toCharArray();
int[] alphabetCount = new int[26];
int length = S.length();
for (int i = 0; i < length; i++) {
alphabetCount[alphabetArr[i] - 'a']++;
}
int max = 0, alphabet = 0, threshold = (length + 1) >> 1;
for (int i = 0; i < alphabetCount.length; i++) {
if (alphabetCount[i] > max) {
max = alphabetCount[i];
alphabet = i;
if (max > threshold)
return "";
}
}
char[] res = new char[length];
int index = 0;
while (alphabetCount[alphabet]-- > 0) {
res[index] = (char) (alphabet + 'a');
index += 2;
}
for (int i = 0; i < alphabetCount.length; i++) {
while (alphabetCount[i]-- > 0) {
if (index >= res.length) {
index = 1;
}
res[index] = (char) (i + 'a');
index += 2;
}
}
return new String(res);
}
}
|
这道题首先的想法就是获取每个字符的个数。
最初的想法,我先取出个数最多的字符,排成一列。再将其他字符填进去。虽然这个思路成功得出,如果存在个数大于总数一半的字符,则无法构成题目要求的字符串。但后续思路却并不好想,当字符个数接近平均时,后续怎么放字符?
正确的思考方向是从整体考虑:字符串有多长,坑位就有多少个。坑位是定的。前一种思考方法,坑位是不定的。
(1)为了达到不相邻的效果,字符肯定是隔一位置放一个,那么刚开始怎么放?放第一个位置还是第二个位置?
(2)从奇数位置个数总是大于等于偶数位值个数(下标从1开始),从第一个位置开始放比较好点。
思路:将字符个数排降序,从最多的字符开始,从第一个位置开始,隔一个放一个。奇数位置放满后,放偶数位置。
多数元素2
给定一个大小为 n 的整数数组,找出其中所有出现超过 ⌊ n/3 ⌋ 次的元素。
https://leetcode.cn/problems/majority-element-ii/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| class Solution {
public List<Integer> majorityElement(int[] nums) {
int[] candidate = new int[2];
int[] vote = new int[2];
int[] count = new int[2];
for(int num:nums){
if(candidate[0]==num){
vote[0]++;
}else if(candidate[1]==num){
vote[1]++;
}else if(vote[0]==0){
candidate[0]=num;
vote[0]++;
}else if(vote[1]==0){
candidate[1]=num;
vote[1]++;
}else{
vote[0]--;
vote[1]--;
}
}
for(int num:nums){
if(vote[0]>0 && candidate[0]==num)
count[0]++;
if(vote[1]>0 && candidate[1]==num)
count[1]++;
}
List<Integer> ans = new ArrayList<>();
if(vote[0]>0 && count[0]> nums.length/3)
ans.add(candidate[0]);
if(vote[1]>0 && count[1]> nums.length/3)
ans.add(candidate[1]);
return ans;
}
}
|
首先看一道相关题目:lc 169 众数
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public int majorityElement(int[] nums) {
int count = 0;
Integer candidate = null;
for (int num : nums) {
if (count == 0) {
candidate = num;
}
count += (num == candidate) ? 1 : -1;
}
return candidate;
}
}
|
采用摩尔投票算法,只需遍历一遍数组就能知道众数。
怎么从「摩尔投票法」拓展到多数元素2?将消除的过程从一个坑位拓展到两个坑位!
个人理解摩尔投票法本质上就是宾果消消乐游戏,每次消除3个不同的数。由于数组长度为n,因此消消乐最多进行[n/3]次。因此,我们想要的答案(超过[n/3]的数字)一定没有被消除完,一定存在最后活下来的两个数当中。 但是,存活的两个数不一定都是想要的真正的答案,最后再遍历确认一下这两个数是不是答案即可。
证明的核心就是抽屉原理。(抽屉原理:N+1个苹果放在N个抽屉,至少有一个抽屉有2个及以上的苹果)
(1)众数
相消的过程其实就是提取一个相异元素对的过程。我们可以构造容量为2的抽屉,这个抽屉只能放不同的元素。
有多少个抽屉?最多 ⌊ n/2 ⌋个罢了。而我们知道,众数是超过 ⌊ n/2 ⌋个的,每个抽屉最多放1个众数,
最后留下来的自然就是众数。
(2)超过 ⌊ n/3 ⌋ 次的元素
其实上面的过程还有一个逻辑,就是众数只有1个。回到本题,超过 ⌊ n/3 ⌋ 次的元素(这里称之为次众数吧)最多只有2个(证明过程留给读者)。
我们可以仿造上面的证明过程,构造容量为3的抽屉,每个抽屉中的元素互不相同,最多有 ⌊ n/3 ⌋个抽屉。那么超过 ⌊ n/3 ⌋的元素自然在相消的过程中留了下来。
算法:构造容量为2的候选集,遍历数组元素,如果当前元素与候选集都不同,则互相消去(放入一个抽屉)。如果当前元素与候选集中的一个元素相同,则那个元素的计数加一。最后检验候选集里的元素是否满足要求。
时间复杂度O(N),空间复杂度O(1)。
(3)拓展:超过 ⌊ n/k ⌋的元素
算法:构造容量为k-1的候选集,重复上面所述的遍历行为,最后检验一下。
证明:依然是构造容量为k的抽屉,每个抽屉中的元素互不相同,最多有 ⌊ n/k ⌋个抽屉。那么超过 ⌊ n/k ⌋的元素自然在相消的过程中留了下来。
四周目 区间贪心
区间贪心原理
区间不相交问题:给定N个开区间,找出尽可能多的开区间,两两不相交。
区间选点问题:给定N个闭区间,确定最少需要几个点,使得每个闭区间都覆盖到点。
区间不相交问题
(1)排序
区间贪心总是要先排序,假设按照左端点升序排序。
(2)从区间包含讲起
如果区间A包含区间B,那么选不相交的区间时,肯定选B,因为B更小,能够让出更多的空间。在刨除了区间包含的情况后,此时各区间的情况是类似阶梯形。
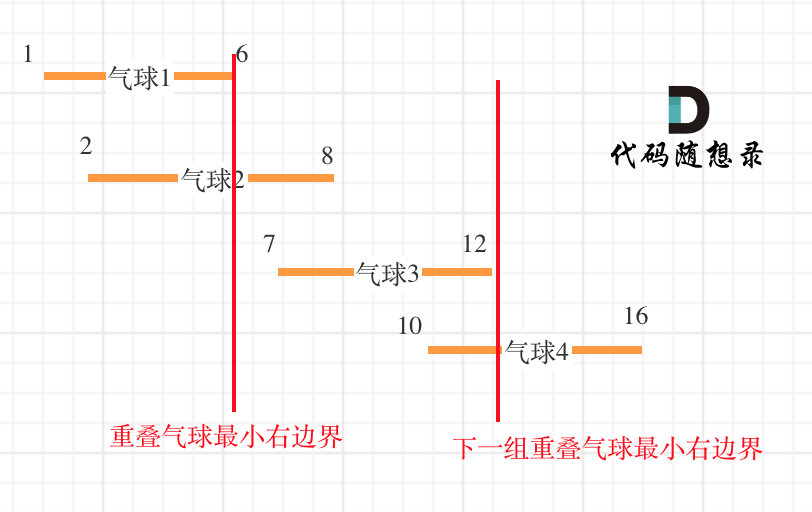
考虑第一段区间的左端点到第二段区间的左端点部分,这一部分是肯定没有重叠的。考虑去掉它,那么第一段区间就包含第二段区间内了,这时候肯定选第一段区间。
(3)策略
按照区间左端点排序,然后总是选择右端点最小的区间。
1
2
3
4
5
6
7
8
9
|
int ans=1;
int last_y = I[0].y;
for(int i=1; i<N; ++i){
if(I[i].x >= last_y){
last_y = I[i].y;
ans++;
}
}
|
区间选点问题
区间选点问题也是同样的,如果存在区间包含的情况,选择被包含的区间,因为它覆盖到了更多的区间。
排序过后,对于第一段相交区间,选哪个点能够让它覆盖尽可能多的区间?是第一个区间的右端点还是第二个区间的左端点?当然是第一个区间的右端点,因为它更靠右,能够覆盖更多区间。
1
2
3
4
5
6
7
8
9
|
int ans=1;
int last_y = I[0].y;
for(int i=1; i<N; ++i){
if(I[i].x > last_y){
last_y = I[i].y;
ans++;
}
}
|
最少数量的箭引爆气球
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
public int findMinArrowShots(int[][] points) {
Arrays.sort(points, (a1, a2) -> {
if(a1[0] == a2[0]) return a1[1] > a2[1] ? 1 : -1;
return a1[0] > a2[0] ? 1 : -1;
});
int ans = 1;
int last_y = points[0][1];
for(int i=1; i<points.length; ++i){
if(points[i][0] > last_y){
ans++;
last_y = points[i][1];
}else{
last_y = Math.min(last_y, points[i][1]);
}
}
return ans;
}
}
|
其实就是找最多的不相交区间。不相交的区间都需要一只箭射。其他与之相交的区间可以通过调箭的位置使之射中。
无重叠区间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));
int ans = 1;
int last_y = intervals[0][1];
for(int i=1; i<intervals.length; ++i){
if(intervals[i][0] >= last_y){
ans++;
last_y = intervals[i][1];
}else{
last_y = Math.min(last_y, intervals[i][1]);
}
}
return intervals.length - ans;
}
}
|
给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
思路:其实就是找最多不相交区间。区间总数减去这个数就是要移除的区间数目。
合并区间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public int[][] merge(int[][] intervals) {
Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));
List<int[]> ans = new LinkedList<>();
int left = intervals[0][0];
int right = intervals[0][1];
for(int i=1; i<intervals.length; ++i){
if(intervals[i][0] > right){
ans.add(new int[]{left, right});
left = intervals[i][0];
}
right = Math.max(right, intervals[i][1]);
}
ans.add(new int[]{left, right});
return ans.toArray(new int[0][0]);
}
}
|
这个就是贪心思路,相交区间一直合并,直到遇到不相交的区间。
划分字母区间
字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。
1
2
3
| - 输入:S = "ababcbacadefegdehijhklij"
- 输出:[9,7,8]
- 解释: 划分结果为 "ababcbaca", "defegde", "hijhklij"。 每个字母最多出现在一个片段中。 像 "ababcbacadefegde", "hijhklij" 的划分是错误的,因为划分的片段数较少。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public List<Integer> partitionLabels(String s) {
int[] jump = new int[26];
for(int i=0; i<s.length();++i){
jump[s.charAt(i)-'a'] = i;
}
List<Integer> list = new ArrayList<>();
int l=0, r=0;
for(int i=0; i<s.length(); ++i){
r = Math.max(r, jump[s.charAt(i)-'a']);
if(i==r){
list.add(r-l+1);
l = r+1;
}
}
return list;
}
}
|
思路:这道题类似合并区间。将每个字母第一次出现的位置看成区间的左端点,最后一次出现的位置看成区间的右端点。那么重叠的区间就必须合并(否则一个字母出现在两个划分中)。
具体实现有技巧。
五周目
单调递增的数字
https://leetcode.cn/problems/monotone-increasing-digits/description/
给定一个非负整数 N,找出小于或等于 N 的最大的整数,同时这个整数需要满足其各个位数上的数字是单调递增。
从后往前调整,如果k+1位的数字小于第k位的数字,那么调整第k+1位的数字为9,第k位数字减一。重复这个过程,直至遍历完。
监控二叉树
这个贪心策略就是:隔一层放一个摄像头。让叶子结点的父亲放置摄像头。

