最长有效括号
https://leetcode.cn/problems/longest-valid-parentheses/
暴力法
首先是暴力法思路:判断字符串每一个偶数长度的子串是否是有效匹配括号,然后记录最大长度。判断一个子串是否是有效匹配的方式是栈(左括号入栈,右括号出栈,如果为有效匹配,最后栈为空)。
动态规划法
dp[i]代表以s[i]为结尾的最长有效括号字符串长度,dp数组的初始值应该为0。
一个字符不能组成有效的括号对,所以为dp[0]为0,然后从s[1]开始往后遍历并同时更新dp数组。
只有右括号才能组成有效括号,注意看下图:
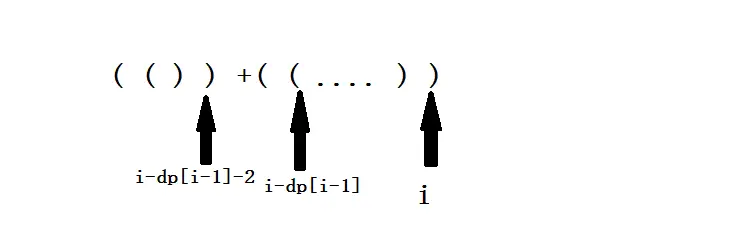
当前遍历到第i位,如果第i-1位是左括号,那么要考虑串连的情况;如果第i-1位是右括号,那么要考虑嵌套+串连的情况。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
public int longestValidParentheses(String s) {
int ans =0;
int[] dp = new int[s.length()];
for(int i=1; i<s.length(); ++i){
if(s.charAt(i)==')'){
if(s.charAt(i)=='('){
dp[i] = 2;
if(i-2>=0) dp[i]+=dp[i-2];
}else{
if(i-dp[i-1]>0 && s.charAt(i-dp[i-1]-1)=='('){
dp[i] = 2 + dp[i-1];
if(i-dp[i-1]-2>=0) dp[i]+=dp[i-dp[i-1]-2];
}
}
ans = Math.max(ans, dp[i]);
}
}
return ans;
}
}
|
这里用动态规划的难点是下标难以搞懂。dp数组的含义是长度,位置i的右括号对应的最长有效括号的左括号位置是i-dp[[i]+1。
栈+动态规划
这将达到N的立方复杂度,有没有其他方法呢?来分析一下可能的括号匹配例子:
将栈修改为存字符的下标,遇到 ‘)’ 则计算栈顶下标差,然后出栈(如果栈空就跳过)。
这个朴素的想法可以应对嵌套括号,无法应对串行括号。根本原因在于忽略了前面的括号。
因此我们增加一个dp数组,用来记录下标i结尾的有效括号长度。计算栈顶下标差的同时还要加上栈顶前一个字符的有效括号长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public int longestValidParentheses(String s) {
Stack<Integer> stk = new Stack<Integer>();
int ans = 0;
int[] dp = new int[s.length()];
for(int i = 0 ,start = 0;i < s.length();i++){
if( s.charAt(i) == '(')
stk.add(i);
else{
if(stk.isEmpty()) continue;
int idx = stk.pop();
if(idx-1>=0)
dp[i] = dp[idx-1] + i-idx+1;
else
dp[i] = i-idx+1;
ans = Math.max(ans, dp[i]);
}
}
return ans;
}
}
|
双指针贪心法
用栈来进行匹配其实就是两个操作:push和pop。我们可以用这两个变量表示对应操作的数量,对于一个有效匹配:
- 在任意时刻,push的数量大于等于pop的数量
- 最后时刻,push的数量等于pop的数量
那么我们就可以用一个left表示左括号的数量,right表示右括号的数量,从左向右遍历,遇到相应括号时增加对应数量,然后进行判断:
- 如果left==right,记录最大数量
- 如果left<right,将这两者清空
但这无法应对((()的例子,因为在我们看来左括号过多并不违法,但有效的括号匹配要求left==right。
换个方向思考,从右到左遍历一遍,此时右括号过多并不违法。结合两者的最大值,就能得到答案了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public int longestValidParentheses(String s) {
int left = 0, right=0, ans=0, ans2=0;
int N = s.length();
for(int i=0; i<N; ++i){
if(s.charAt(i) == '(') left++;
else right++;
if(left == right) ans = Math.max(ans, 2*right);
else if (right > left){
left=0;
right=0;
}
}
left = right =0;
for(int i=0; i<N; ++i){
if(s.charAt(N-1-i) == '(') left++;
else right++;
if(right == left) ans2 = Math.max(ans2, 2*left);
else if( left > right){
left=0;
right=0;
}
}
return Math.max(ans, ans2);
}
}
|
